Functions | |
| I32 | rlc_moments (U16 *r0, moment *mx, U32 n) |
| Calculate Moments of Order 0, 1, 2 for Labelled RLC. More... | |
| I32 | rlc_moments3 (U16 *rl0, moment *mq, U32 n) |
| Calculate Moments of Order 0, 1, 2 and 3 for Labelled RLC. More... | |
| F32 | mom_calc_area (moment *mx) |
| Calculate Area from Moments. More... | |
| F32 | mom_calc_cgx (moment *mx) |
| Calculate Center of Gravity X-Coordinate from Moments. More... | |
| F32 | mom_calc_cgy (moment *mx) |
| Calculate Center of Gravity Y-Coordinate from Moments. More... | |
| F32 | mom_calc_angle (moment *mx) |
| Calculate Angle of Inertial Axis from Moments (Result in Degrees). More... | |
| F32 | mom_calc_rad (moment *mx) |
| Calculate Angle of Inertial Axis from Moments (Result in Radiants). More... | |
| F32 | mom_calc_ecc (moment *mx) |
| Calculate Object Eccentricity from Moments. More... | |
| F32 | mom_calc_ellipse_a (moment *mx) |
| Calculate Ellipse Half-Parameters. More... | |
| F32 | mom_calc_ellipse_b (moment *mx) |
| Calculate Ellipse Half-Parameters. More... | |
| F32 | mom_calc_phi1 (moment *mx) |
| Calculate Hu Moments. More... | |
| F32 | mom_calc_phi2 (moment *mx) |
| Calculate Hu Moments. More... | |
| F32 | mom_calc_phi3 (moment *mx) |
| Calculate Third Hu Moment. More... | |
| F32 | mom_calc_phi4 (moment *mx) |
| Calculate Fourth Hu Moment. More... | |
| F32 | mom_calc_ai1 (moment *mx) |
| Calculate Affine Invariant Moment 1. More... | |
| F32 | mom_calc_ai2 (moment *mx) |
| Calculate Affine Invariant Moment 2. More... | |
| F32 | mom_calc_ai3 (moment *mx) |
| Calculate Affine Invariant Moment 3. More... | |
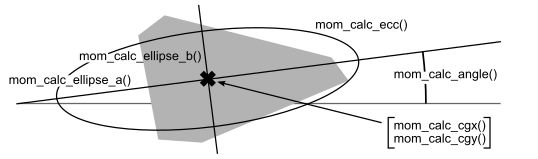
For a description see the section Moments.
The function calculates the centralized moments of order 0, 1 and 2 for the labelled runlength code rlc. The centralized moments may be used to calculate useful features present in the RLC. For example the moment  is equal to the total pixel area of the object. With moments
is equal to the total pixel area of the object. With moments 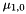 and
and  , the center of gravity for the object can be calculated by dividing these values by
, the center of gravity for the object can be calculated by dividing these values by  . Higher moments may be used to calculate translation-, rotation- and scaling-invariant object features. The output of the function is stored in the struct array
. Higher moments may be used to calculate translation-, rotation- and scaling-invariant object features. The output of the function is stored in the struct array mom. All values of this struct are stored in our proprietary multi-precision integer format. Since there are additional functions available to calculate all meaningful features, it is not necessary to use these values directly. The definition of the moment struct:
Moments of order 3 in this struct are not written with this function. The function rlc_moments() only calculates moments up to the second order. Moments of order 3 can be calculated using function rlc_moments3(). Please refer to Gonzalez, Wintz: "Digital Image Processing", Addison-Wesley 1977 pp. 354ff for the definition of the moments.
Input variables for the function:
| rl0 | Pointer to Labelled RLC (Input to the Function). |
| mq | Array of Struct (Moment Struct) / Function Output. |
| n | Number of Array Elements in mom. The function checks wether this number is sufficiently high for all objects in the RLC. If not, the function returns with an error code. |
On success, the function returns the number of objects in the RLC. This value may be used to address the output struct array. The standard error code is returned on error: RLC is unlabelled or it contains more objects than n.
| ERR_SLC | if RLC is Unlabelled. |
| ERR_RLC_ONOVR | if an Object Number Overrun occured. |
| ERR_RLC_MEM | if Memory Allocation Fails. |
| Object Count | on Success. |
The function calculates the centralized moments of order 0 through 3 for the labelled runlength code rlc. The centralized moments may be used to calculate useful features present in the RLC. For example the moment  is equal to the total pixel area of the object. With moments
is equal to the total pixel area of the object. With moments 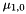 and
and  , the center of gravity for the object can be calculated by dividing these values by
, the center of gravity for the object can be calculated by dividing these values by  . Higher moments may be used to calculate translation-, rotation-, scaling- and even affine-invariant object features. The output of the function is stored in the struct array
. Higher moments may be used to calculate translation-, rotation-, scaling- and even affine-invariant object features. The output of the function is stored in the struct array mom. All values of this struct are stored in our proprietary multi-precision integer format. Since there are additional functions available to calculate all meaningful features, it is not necessary to use these values directly. The definition of the moment struct:
The function rlc_moments3() calculates moments up to the third order. Please refer to Gonzalez, Wintz: "Digital Image Processing", Addison-Wesley 1977 pp. 354ff for the definition of the moments.
Input variables for the function:
| rl0 | Pointer to Labelled RLC (Input to the Function). |
| mq | Array of Struct (Moment Struct) / Function Output. |
| n | Number of Array Elements in mom. The function checks whether this number is sufficiently high for all objects in the RLC. If not, the function returns with an error code. |
On success, the function returns the number of objects in the RLC. This value may be used to address the output struct array. The standard error code is returned on error: RLC is unlabelled or it contains more objects than n.
| ERR_SLC | if RLC is Unlabelled. |
| ERR_RLC_ONOVR | if an Object Number Overrun occured. |
| ERR_RLC_MEM | if Memory Allocation Fails. |
| Object Count | on Success. |
The function mom_calc_area() returns the pixel count of the object.
The functions mom_calc_cgx() and mom_calc_cgy() compute the x- and y-coordinates of the center of gravity for the object with the centralized moments given by mom. The output of the funtion is a float value with subpixel accuracy.
The functions mom_calc_cgx() and mom_calc_cgy() compute the x- and y-coordinates of the center of gravity for the object with the centralized moments given by mom. The output of the funtion is a float value with subpixel accuracy.
The function computes the angle of the inertial axis (minimum moment of inertia) for the object with the centralized moments given by mom. This may be used as the main object orientation, e.g. for robot applications. The output of the function is a float value with subangle accuracy ranging from 0.0 to 179.9 degrees. A value of 0 means, that the object is oriented parallel to the (horizontal) x-axis, '90' means it is parallel to the y-axis. The user must be careful: Since the output does not cover the full range from 0 to 360 degrees, it is not possible to differentiate mirrored positions of the object. The function is also useless for objects with circular symmetry, e.g. for disks, squares and the like. Use the function mom_calc_ecc() to see if the object has some kind of eccentricity which is necessary for a unique inertial axis.
The function computes the angle of the inertial axis (minimum moment of inertia) for the object with the centralized moments given by mom. This may be used as the main object orientation, e.g. for robot applications. The output of the funtion is a float value with subangle accuracy ranging from 0.0 to π. 0 means, the object is oriented parallel to the (horizontal) x-axis, π/2 means it is parallel to the y-axis. The user must be careful: Since the output does not cover the full range from 0 to 2π, it is not possible to differentiate mirrored positions of the object. The function is also useless for objects with circular symmetry, e.g. for disks, squares and the like. Use the function mom_calc_ecc(), to see if the object has some kind of eccenticity which is necessary for a unique inertial axis.
The function computes the eccentricity for the object with the centralized moments given by mom. This may be used as the main object orientation, e.g. for robot applications. The output of the funtion is a float value with ranging from 0.0 to 1.0. '0.0' means, the object is totally symmetric, like a disk or a square, '1.0' means the object is totally eccentric, like a needle. The eccentricity for an ellipsoid with half-diameter a and b, the eccentricity would be (a - b)/(a + b).

The functions mom_calc_ellipse_a() and mom_calc_ellipse_b() calculate the half-parameters a and b of the equivalent ellipse for the object with the centralized moments given by mom.
The functions mom_calc_ellipse_a() and mom_calc_ellipse_b() calculate the half-parameters a and b of the equivalent ellipse for the object with the centralized moments given by mom.
The functions mom_calc_phi1() and mom_calc_phi2() compute the first two Hu moments.
With the definition:
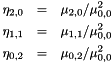
the first two Hu moments are defined as follows:
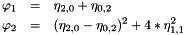
The functions mom_calc_phi1() and mom_calc_phi2() compute the first two Hu moments.
With the definition:
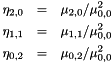
the first two Hu moments are defined as follows:
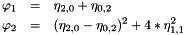
The function computes the third Hu moment.
With the definition:
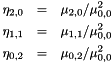
the third Hu moment is defined as follows:
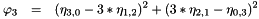
The function computes the fourth Hu moment.
With the definition:
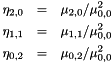
the fourth Hu moment is defined as follows:

The function computes the first Affine Invariant Moment.
With the definition:
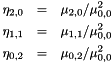
the first Affine Invariant Moment is defined as follows:

Affine Invariants are fully explained in Flusser, Suk, Zitova: "Moments and Moment Invariants in Pattern Recognition", Wiley 2009, pp 60 ff.
The function computes the second Affine Invariant Moment.
Affine Invariants are fully explained in Flusser, Suk, Zitova: "Moments and Moment Invariants in Pattern Recognition", Wiley 2009, pp 60 ff.
The function computes the third Affine Invariant Moment.
Affine Invariants are fully explained in Flusser, Suk, Zitova: "Moments and Moment Invariants in Pattern Recognition", Wiley 2009, pp 60 ff.